
Эффект Моцарта: музыка помогает учиться или мешает?
Учёные десятилетиями пытаются ответить на вопрос, полезно ли включать фоновую музыку на учебных занятиях. Рассказываем, что об этом известно.

На ошибках правда учатся? Исследователи уверяют, что нет — но это можно исправить
Многие преподаватели и тренеры убеждены в учебной пользе от провалов и неудач. Но чтобы эта польза действительно была, нужно соблюсти ряд условий.
Методические особенности постановки обучения математике в 5-6 классах, направленного на развитие одарённых детей

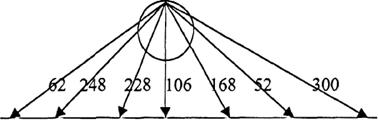
1. Какая птица в нашей стране самая высокая? Решение данных заданий поможет ответить на данный вопрос. 1) 74 +32; 2) 59 + 3; 3) 95 – 43; 4)186 + 42; 5)502 – 202; 6)42 +206; 7)175 – 7.
2. Узнайте ее высоту. Для этого впишите в свободные клетки таблицы такие числа, чтобы квадрат стал магическим. Сумма найденных четырех чисел поделенная на 10 и укажет вам высоту птицы (в дециметрах).
4737
41 49
45
Ключ к заданию В
Карточка С – задание для группы С
(Тип задачи: творческая; для одаренных)
Вариант ответа (заполняется в ходе поиска решения задачи)
1)Название самой крупной птицы в мире вы расшифруете, если выполните действия:
41 – 22; 119 –99; 18 + 0; 1002 – 978;
16 + 5; 3 + 33 + 333 – 350.
Ответы замените буквами
Составьте математический паноптикум, условием которого служат следующие данные: самой крупной птицей в мире является африканский страус. Страус не летает, это очень странно - птица и не летает, но зато она очень быстро бегает, являясь рекордсменом по бегу
2) Продолжительность жизни Вам поможет узнать ответ данного уравнения: 10003 – y = 9968;
3) Найдя значение выражения
3030 – (2910 + 30), вы узнаете вес этой птицы в кг;
4) Пользуясь материалами карточки определите вес одного куриного яйца.
среди птиц. Его длинные и сильные ноги с огромной скоростью носят по саваннам и пустыням. Велика и сила этой птицы. Могучая лапа служит страусу неплохим оружием – одним ударом он может не только свалить человека с ног, но и убить его. Масса страуса – 90 кг. Средняя продолжительность жизни – 35 лет. Масса одного яйца страуса 2 кг, оно заменяет 25 куриных яиц. Примечание: математический паноптикум – это музей, в котором собраны уникальные нематематические объекты на математической основе.
Примечание: нумерация графы деятельность учащихся соответствует нумерации обобщенного приема поиска решения задач.
Ход урока
|
Этапы |
Деятельность учителя |
Деятельность учащихся |
|
1 II III IV |
1) Формулирует задание с кодо-позитива. 2)Предлагает учащимся записать краткое условие задачи, используя кодопозитив. 3)Совместно с учащимися принимается идея записи условия задачи на математический язык. 4)Принимает идеи групп по решению задач. 5) Просит всех в тетради записать ответ левой рукой. 1)Выдает индивидуальные задания каждой группе. 2)Координирует работой группы А и консультирует при необходимости группу В. 3)«Подводит» к обобщенному приему поиска решения задачи. 4)Предлагает рассмотреть приложение ключей А и В. Предлагает послу- шать доклад. Записывает домаш- нее задание на доске и поясняет его. Задает вопросы уча- щимся: Чему Вы на- учились на уроке? Где в практической жизни Вам пригодятся знания свойств сложения и вычитания натураль- ных чисел ? Комментирует оценки. |
Работают в группах А1, А2, А3: 1) изучают содержание задачи, используя рисунок, делают краткую запись (задание воспроизводят на память); 2) уточняют формулировку задачи, определяя, что «пес» и «собачонка» - слова-синонимы; 6) вспоминают, что данная задача напоминает уравнение, прием решения которой известен, сравнивают их и на этой основе составляют план решения задачи: вводят обозначения: А–акробат; С–собачонка; Б–бочонок; М–моток; Я–ягненок. 7) использует отмеченный прием аналогии, который позволяет решить данную задачу: А + С = 2Б, а С = 2М и Я + М = Б; А= ХЯ? Следовательно, А + С = 2Я +2М. Учитывая, что С = 2 М, запишем: А + 2М = 2Я + 2М, А = 2Я. Ответ: акробат весит ровно два ягненка (команды выставляют по одному представителю для записи ответа левой рукой (оценивается кто быстро и правильно запишет ответ). Примечание: учащиеся III-го уровня в своих группах выполняют роль консультантов в ходе всей работы по решению данной задачи. Работают в группах А, В, С. Учащиеся группы А: изучают задание, используют краткую запись; определяют, что тип задачи паноптикума, напоминает кроссворд и вспоминают известный прием его решения; 5) разделяют условие задачи на части, составляют план решения каждой из них, затем объединяют ответы, что позволяет найти решение задачи, т.к. поиск решения оказывается верным. Решение задачи по карточке А записывается в тетрадь. Один учащийся группы А оформляет решение на доске: 1025 – Х = 125 Х = 1025 – 125 X = 900; 458 + 333 + 11 + 1 = 803; 3)Сколько лет составляют два века? Ответ: 200лет; 4)(1203 – 1003) – (1515 – 1509) = 1200. Ответы заданий являются ключами к слову «бобр». Учащиеся группы В: 1) Изучают задание, используют краткую запись; 2) определяют, что тип задачи панопти -кума, напоминает кроссворд и вспоминают известный прием его решения; 5) разделяют условие задачи на части, составляют план решения каждой из них, затем объединя- ют ответы, что позволяет найти решение задачи, т.к. поиск решения оказывается верным. Решение по карточке группы В: 1) 74 + 32 = 106, 2) 59 + 3 = 62, 3) 95 – 43 =52, 186 + 42 = 228, 5)502 – 202 = 300, 6) 42 + 206 = 248, 7)175 – 7 = 168, Ответы заданий являются ключами к слову «журавль». Решение: 473739 334149 434535 33 + 43 + 35 + 39 = 150, 150:10 = 15. Ответ: Самая высокая птица в нашей стране – журавль, высота которой – 15 дм. Учащиеся группы С (работают каждый самостоятельно и в конце урока сдают свои работы для проверки учителю); 1) изучают содержание задачи, самостоятель- но предлагают свое видение задачи в иллюстрации; 2) уточняют формулировку задачи, чтобы при решении задачи можно было вспомнить прием решения; 3) преоб- разуют информацию с учетом специфики данной задачи; 8) преобразуют условие задачи с целью его сближения с вопросом; 12) полностью используют содержание текста задачи; 14) ставят перед собой такие вопросы, которые: а) позволяют осмыслить задачу с новой (неожиданной) точки зрения, б) позволяют использовать полученные знания и опыт решения других задач, в) побуждают к самоконтролю; 16) анализируют все возможные реше- ния, оценивают их эффективность. Решение по карточке группы С (вариант ответа): 1) 41 – 22 = 19 (С); 119 – 99 = 20 (Т); 18 + 0 = 18 (Р); 1002 – 978 – 23 = 1 (А); 16 + 5 = 21 (У); 3 + 33 + 333 – 350 = 19 (С). 2)Решение: У = 10003 – 9968; У = 35. 3) Найдя значение выражения 3030 - (2910 + 30 ) вы узнаете вес этой птицы в кг (90); 4) Пользуясь материалами карточки определите вес одного куриного яйца. Решение: 2000 : 25 = 80 (г). Записывается ответ. Ученик выступает с докладом на тему: «Числа натурального ряда и мистические суеверия» (учащийся III-го уровня), доводит до своих одноклассников результат своей творческой работы; отвечает на вопросы, обобщая полученный опыт по теме. А: № 226 (в), 228 (б), 230, 280; В: № 232, 234, 288; С: № 236 (творческая задача исторического содержания), 271 (задача на выделение существенного и поиск закономерностей) (учебник математики, 5 класс, Н. Я. Виленкин) Предполагаемые ответы: 1) дальнейшее общее и математическое развитие; использовать в быту (считать, сравнивать, уметь обобщать, .), не верить суевериям. 2) использовать математические знания по теме «сложение и вычитание натуральных чисел» при нахождении ответов на вопросы нематематического характера. |
Особенности представлений о геометрических фигурах и форме предмета у
старших дошкольников
Исследуя особенности восприятия геометрических фигур детьми А.А. Столяр приходит к вводу, что геометрическое мышление" вполне возможно развить еще в дошкольном возрасте. В развитии "геометрических знаний" у детей прослеживается несколько различных уровней. Первый уровень характеризуе ...
Философские и педагогические взгляды французских материалистов XVIII в
Гельвеций (1715—1771) прославился как автор книги “Об уме”, которая вышла в 1758 г. и вызвала яростные нападки со стороны всех сил реакции, правящих кругов. Книга была запрещена и приговорена к сожжению. Еще более обстоятельно Гельвеций развил свои идеи в книге “О человеке, его умственных способнос ...
Социально-бытовая ориентировка: понятие и основные характеристики
амблиопия косоглазие слуховой дошкольник Под социально-бытовой ориентировкой подразумевается комплекс знаний и умений, непосредственно связанный с организацией собственного поведения и общения с окружающими людьми в различных социально-бытовых ситуациях. В своем общем смысле социально-бытовая ориен ...
Как Тейлор Свифт стала человеком года... в образовании

Ей уже посвящают учебные курсы в Гарварде, Стэнфорде и других известных вузах! В том числе — юридические и предпринимательские. Рассказываем, почему.
Разделы
- Главная
- Основы педагогической психологии
- История развития педагогической мысли
- Мировые дидактические концепции
- Педагогическое мастерство
- Управление системой образования
- Принципы воспитания
- Раздел
