Методы оценки надежности

Как уже говорилось выше, надежность теста характеризует степень устойчивости результатов тестирования каждого испытуемого. Методы оценки надежности заключаются в вычислении коэффициента надежности разными способами.

Метод 1 – метод половинного деления. Тест делится на две равные части и подсчитывается сумма баллов, набранных испытуемыми по каждой из половин. Полученные величины коррелируются между собой по формуле Пирсона [21]. Полученный коэффициент показывает надежность теста при коррелировании его половин, он говорит о внутренней состоятельности теста.

А. Коэффициент надежности теста вычисляется по формуле Спирмана-Брауна [21]:

,

где - коэффициент надежности теста по двум половинам.

В. Значение коэффициента надежности в этом методе интерпретируется следующим образом: если коэффициент надежности принимает значение от 0,8 до 1, то надежность хорошая, от 0,5 до 0,8 – удовлетворительная и менее 0,5 – неудовлетворительная.

2-й метод – метод подсчета средней корреляции заданий теста.

А. Надежность этим методом вычисляется по формуле [21]:

,

где - средняя корреляция, - сумма средних значений в корреляционной таблице [21, стр.13, табл.2], - общее число заданий.

В. Результаты вычисления в этом методе интерпретируются также как и в предыдущем.

3-й метод.

А. Коэффициент надежности вычисляется по формуле Кюдера-Ричардсона [20]:

,

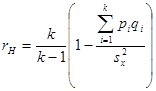где - число заданий в тесте, - сумма дисперсий заданий теста, - дисперсия.

В. Результаты интерпретируются аналогично предыдущим методам.

4-й метод - метод оценки высоких и низких достижений группы. Для расчета коэффициента надежности используется разбиение тестируемых на две группы. При достаточно большом количестве испытуемых каждая из этих групп составляет примерно 0,27 от общего количества.

А. Коэффициент надежности рассчитывается по формуле [20]:

,

где и - средние достижения групп с наиболее высокими и наиболее низкими результатами соответственно (группа испытуемых делится на две равные части) [20].

В. Результаты интерпретируются аналогично предыдущим методам.

Вывод: мы рассмотрели четыре метода нахождения надежности. В трех методах используют корреляционную связь, в одном учитывают достижения группы. Заметим, что коэффициенты надежности найденные разными методами отличаются. Приведем пример таблицы значений коэффициента надежности, полученный разными способами, который рассчитывался по результатам теста ЕГЭ.

Таблица 2. Значения коэффициента надежности, рассчитанного разными способами.

Методика работы по коррекции фонематического восприятия у детей дошкольного возраста с ОНР третьего уровня
Все содержание коррекционно-логопедической работы должно строиться в соответствии с принципами логопедии. Принцип системности опирается на представление о речи, как о сложной функциональной системе, структурные компоненты которой находятся в тесном взаимодействии. В связи с этим необходимо подбират ...

Определение и структура психологической готовности кшкольному обучению
Период от рождения до поступления в школу является возрастом наиболее стремительного физического и психического развития ребенка, первоначального формирования качеств и свойств, делающих его человеком. Особенностью этого периода является то, что именно он обеспечивает общее развитие, служащее фунда ...

Классификация дидактических игр
Классифицировать игровые уроки особенно сложно. Игровые технологии обучения отличаются исключительным разнообразием. Основной мотив игры – её процесс, а не результат. Это усиливает их развивающее значение, но делает менее очевидным образовательный эффект. Несомненно, у игровых уроков есть и образов ...